一种时空轨迹相似度计算方法及系统

本发明公开一种时空轨迹相似度计算方法及系统，所述方法包括：步骤1，定义距离转角率，刻画用户兴趣点的特征；步骤2，根据经验阈值，识别用户兴趣点；根据轨迹的用户兴趣点计算其公共兴趣点；步骤3，计算分段之间的相似度以及不相似度，其中所述分段为两个公共兴趣点之间的分段；通过定义分段时间、相似分段、相似路线，计算轨迹之间的相似度以及不相似度，从而得到轨迹相似度。

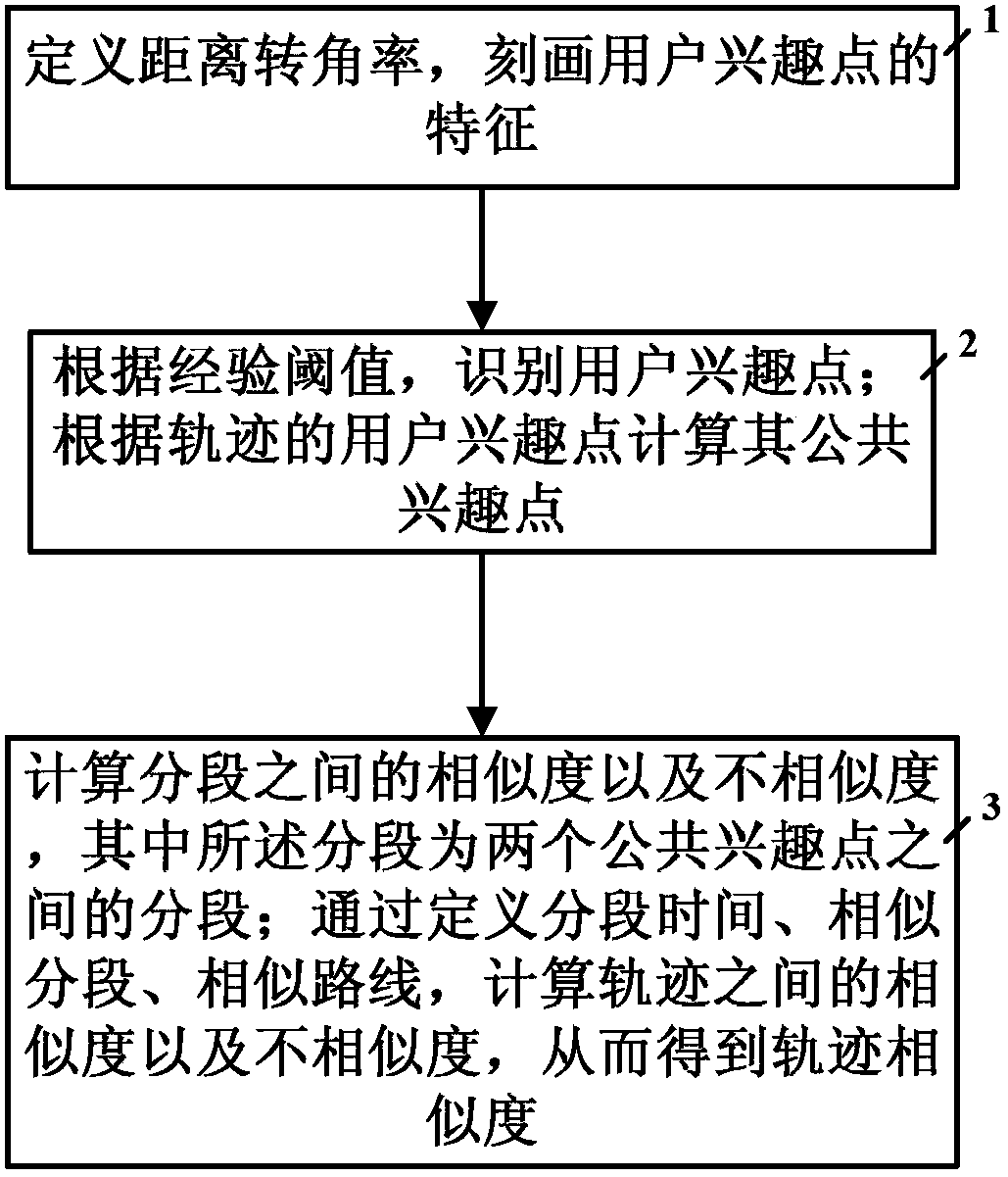
1.一种时空轨迹相似度计算方法，其特征在于，包括：步骤1，定义距离转角率，刻画用户兴趣点的特征；步骤2，根据经验阈值，识别用户兴趣点；根据轨迹的用户兴趣点计算其公共兴趣点；步骤3，计算分段之间的相似度以及不相似度，其中所述分段为两个公共兴趣点之间的分段；通过定义分段时间、相似分段、相似路线，计算轨迹之间的相似度以及不相似度，从而得到轨迹相似度；其中，所述步骤1还包括：步骤21，定义p_i-1、p_i到p_i+1的距离转角率LATatio(p(i-1),p(i),p(i+1))，其中p_i-1、p_i、p_i+1分别为用户兴趣点,i为兴趣点序号；距离转角率公式如下： LATatio ( p ( i - 1 ) , p ( i ) , p ( i + 1 ) ) = LARatio ( v → ( p i - 1 , p i ) , v → ( p i , p i + 1 ) ) = 1 - cos ( θ i ) ϵ + | | v → ( p ( i ) , p ( i + 1 ) ) | | ]]> 其中，θ_i为兴趣点列i的角度,ε是满足下述条件的任意一个常量： 0 < ϵ < min { | | v → ( p ( i ) , p ( i + 1 ) ) | | } ]]> 且 ϵ + min { | | v → ( p ( i - 1 ) , p ( i ) ) | | } < min sec { | | v → ( p ( i - 1 ) , p ( i ) ) | | } ]]> 其中，是向量的模，是的第二小值；如果ε满足以下不等式： 0 < ϵ < min th { | | v → ( p ( i - 1 ) , p ( i ) ) | | } ]]> 且 ϵ + min sec { | | v → ( p ( i - 1 ) , p ( i ) ) | | } < min th { | | v → ( p ( i - 1 ) , p ( i ) ) | | } ]]> 其中，sec和th分别表示第二和第三，因此是的第三小值，为向量；所述步骤2还包括：步骤41，如果ratio＞ρ，这里ρ是一个经验阈值，则认为兴趣点p(i)和p(i+1)是同一个兴趣点，IS(j)表示轨迹中的j个兴趣点；为了计算轨迹的相异程度，用IP(j)表示IS(j)，IP(j)＝(Long(j),Lat(j),T(j))是IS(j)中兴趣点的加权平均,其中j是兴趣点的编号， Long ( j ) = Σ i = 1 n is rati o i Σ i = 1 n is ratio ( i ) · long ( i ) , ]]> Lat ( j ) = Σ i = 1 n is rati o i Σ i = 1 n is ratio ( i ) · lat ( i ) , ]]> T ( j ) = Σ i = 1 n is rati o i Σ i = 1 n is ratio ( i ) · t ( i ) ]]> 其中ratio_i为兴趣点i的距离转角率，ratio(i)为兴趣点(i)的距离转角率，n_is为第j个兴趣点所涉及的距离转角率的个数，long(i)为兴趣点i的精度，lat(i)为兴趣点i的纬度，t(i)为兴趣点i的时间,Long(j)为兴趣点j的精度，Lat(j)为兴趣点j的纬度，T(j)为兴趣点j的时间；步骤42，如果两个兴趣点IP(i)和IP(j)之间的距离小于d_p，称这两个兴趣点为公共兴趣点CoIP，d_p根据具体赋值而变化；所述步骤3还包括：步骤51，位于CoIP(i)和CoIP(i+1)中间的部分为tra(1)中的分段，记做seg_tra(i)；下述公式计算分段的不相似程度：dif_vector(seg_i(tra₁),seg_i(tra₂))＝Vdif_vector(seg_i(tra₁),seg_i(tra₂))+|n1_in-n2_in|其中，Vdif_vector(seg_i(tra₁)，seg_i(tra₂))＝||vq₁(seg_i(tra₁))-vq₁(seg_i(tra₂))||+||vq₂(seg_i(tra₁))-vq₂(seg_i(tra₂))||Vdif_vector为相似路线，tra₁为兴趣点列1，tra₂为兴趣点列2，seg_i(tra₁)为兴趣点列1的分段，seg_i(tra₂)为兴趣点列2的分段，n1_in为兴趣点列1中两个正常兴趣点之间非公共兴趣点的数量，n2_in为兴趣点列2中两个正常兴趣点之间非公共兴趣点的数量,其中公共兴趣点形成轨迹分段，将轨迹各分段分为2个分区，相邻两个分段构成4个分区，Vq1()和Vq2()分别为连接1、3分区和2、4分区的向量，Vq1()和Vq2()的走向与轨迹走向相同。
2.如权利要求1所述的时空轨迹相似度计算方法，其特征在于，所述步骤3还包括：步骤62，分段时间，是指用户从一个CoIP到另一个CoIP的间隔时间，如果CoIP_i＝(Long_i,Lat_i,T_i)，且CoIP_i+1＝(Long_i+1,Lat_i+1,T_i+1)，那么T_i-T_i+1为CoIP_i和CoIP_i+1在轨迹中的分段时间，Long_i+1为兴趣点的精度，Lat_i+1为兴趣点的纬度，T_i+1为兴趣点的时间；相似分段，是令seg_i(tra₁)和seg_i(tra₂)分别为tra₁和tra₂中的分段，称seg_i(tra₁)和seg_i(tra₂)为相似分段，当两个分段之间IP的数量相等；两个分段之间的分段时间的绝对差值小于一个常数，即|(T_i(tra₁)T_i+1(tra₁))-(T_i(tra₂)T_i+1(tra₂))|＜t_p其中(T_i(tra₁)T_i+1(tra₁))为兴趣点列1的分段时间，(T_i(tra₂)T_i+1(tra₂))为兴趣点列2的分段时间，t_p为常数；相似路线，由分段组成，如果有多个连续的相似分段，则为相似路线；假设r_i和r_j是相似路线，则认为两条路线没有区别，即Vdif_vector(r_i(tra₁),r_j(tra₂))＝0，其中r_i(tra₁)为兴趣点列1的路线，r_j(tra₂)为兴趣点列2的路线；下述公式计算轨迹之间的不相似度： dif ( tra 1 , tra 2 ) = Σ i = 1 n p ω i dif vector ( seg i ( tra 1 ) , seg i ( tra 2 ) ) + max { n 1 ex , n 2 ex } ]]> 其中，max{n_1ex,n_2ex}是n_1ex和n_2ex的最大值，n_1ex是tra(1)位于公共点之外的non-COIPs数量，n_2ex是tra(2)位于公共点之外的non-COIPs数量，n_p是用户兴趣点的数量，在tra(1)中有两个位于公共点之外的non-CoIPs，因此n_1ex＝2，tra(2)中位于公共点之外的non-CoIPs的数量为1，n_2ex＝1，因此max{n_1ex,n_2ex}＝2； ω i = ( Len i ( tra 1 ) Len ( tra 1 ) · Len i ( tra 1 ) + Len i ( tra 2 ) Len ( tra 2 ) · Len i ( tra 2 ) ) Len ( tra 1 ) + Len ( tra 2 ) ]]> Len_i(tra₁)表示seg_i(tra₁)的长度，Len(tra₁)是tra₁的长度，Len_i(tra₂)表示seg_i(tra₂)的长度，Len(tra₂)是tra₂的长度，seg_i的距离与长度的含义不同，seg_i(tra₁)的距离是CoIP_i和CoIP_i+1之间的直线距离，而长度是用户从CoIP_i走到CoIP_i+1的路程。
3.一种时空轨迹相似度计算系统，其特征在于，包括：定义转角率模块，用于定义距离转角率，刻画用户兴趣点的特征；兴趣点模块，用于根据经验阈值，识别用户兴趣点；根据轨迹的用户兴趣点计算其公共兴趣点；相似度匹配模块，用于计算分段之间的相似度以及不相似度，其中所述分段为两个公共兴趣点之间的分段；通过定义分段时间、相似分段、相似路线，计算轨迹之间的相似度以及不相似度，从而得到轨迹相似度；其中，所述定义转角率模块还包括：定义p_i-1、p_i到p_i+1的距离转角率LATatio(p(i-1),p(i),p(i+1))，其中p_i-1、p_i、p_i+1分别为用户兴趣点；距离转角率公式如下： LATatio ( p ( i - 1 ) , p ( i ) , p ( i + 1 ) ) = LARatio ( v → ( p i - 1 , p i ) , v → ( p i , p i + 1 ) ) = 1 - cos ( θ i ) ϵ + | | v → ( p ( i ) , p ( i + 1 ) ) | | ]]> 其中，θ_i为兴趣点列i的角度，ε是满足下述条件的任意一个常量： 0 < ϵ < min { | | v → ( p ( i ) , p ( i + 1 ) ) | | } ]]> 且 ϵ + min { | | v → ( p ( i - 1 ) , p ( i ) ) | | } < min sec { | | v → ( p ( i - 1 ) , p ( i ) ) | | } ]]> 其中，是向量的模，是的第二小值；如果ε满足以下不等式： 0 < ϵ < min th { | | v → ( p ( i - 1 ) , p ( i ) ) | | } ]]> 且 ϵ + min sec { | | v → ( p ( i - 1 ) , p ( i ) ) | | } < min th { | | v → ( p ( i - 1 ) , p ( i ) ) | | } ]]> 其中，sec和th分别表示第二和第三，因此是的第三小值，为向量；所述兴趣点模块还包括：经验阈值模块，用于如果ratio＞ρ，这里ρ是一个经验阈值，则认为兴趣点p(i)和p(i+1)是同一个兴趣点，IS(j)表示轨迹中的j个兴趣点；为了计算轨迹的相异程度，用IP(j)表示IS(j)，IP(j)＝(Long(j),Lat(j),T(j))是IS(j)中兴趣点的加权平均,其中j是兴趣点的编号， Long ( j ) = Σ i = 1 n is rati o i Σ i = 1 n is ratio ( i ) · long ( i ) , ]]> Lat ( j ) = Σ i = 1 n is rati o i Σ i = 1 n is ratio ( i ) · lat ( i ) , ]]> T ( j ) = Σ i = 1 n is rati o i Σ i = 1 n is ratio ( i ) · t ( i ) ]]> 其中ratio_i为兴趣点i的距离转角率，ratio(i)为兴趣点(i)的距离转角率，n_is为第j个兴趣点所涉及的距离转角率的个数，long(i)为兴趣点i的精度，lat(i)为兴趣点i的纬度，t(i)为兴趣点i的时间,Long(j)为兴趣点j的精度，Lat(j)为兴趣点j的纬度，T(j)为兴趣点j的时间；距离模块，用于如果两个兴趣点IP(i)和IP(j)之间的距离小于d_p，称这两个兴趣点为公共兴趣点CoIP，d_p根据具体赋值而变化；所述相似度匹配模块还包括：分段模块，用于位于CoIP(i)和CoIP(i+1)中间的部分为tra(1)中的分段，记做seg_tra(i)；下述公式计算分段的不相似程度：dif_vector(seg_i(tra₁),seg_i(tra₂))＝Vdif_vector(seg_i(tra₁),seg_i(tra₂))+|n1_in-n2_in|其中，Vdif_vector(seg_i(tra₁)，seg_i(tra₂))＝||v_q1(seg_i(tra₁))-vq₁(seg_i(tra₂))||+||v_q2(seg_i(tra₁))-v_q2(seg_i(tra₂))||，Vdif_vector为相似路线，tra₁为兴趣点列1，tra₂为兴趣点列2，seg_i(tra₁)为兴趣点列1的分段，seg_i(tra₂)为兴趣点列2的分段，n1_in为兴趣点列1中两个正常兴趣点之间非公共兴趣点的数量，n2_in为兴趣点列2中两个正常兴趣点之间非公共兴趣点的数量，其中公共兴趣点形成轨迹分段，将轨迹各分段分为2个分区，相邻两个分段构成4个分区，Vq1()和Vq2()分别为连接1、3分区和2、4分区的向量，Vq1()和Vq2()的走向与轨迹走向相同。
4.如权利要求3所述的时空轨迹相似度计算系统，其特征在于，所述相似度匹配模块还包括：相似度运算模块，用于分段时间，是指用户从一个CoIP到另一个CoIP的间隔时间，如果CoIP_i＝(Long_i,Lat_i,T_i)，且CoIP_i+1＝(Long_i+1,Lat_i+1,T_i+1)，那么T_i-T_i+1为CoIP_i和CoIP_i+1在轨迹中的分段时间，Long_i+1为兴趣点的精度，Lat_i+1为兴趣点的纬度，T_i+1为兴趣点的时间；相似分段，是令seg_i(tra₁)和seg_i(tra₂)分别为tra₁和tra₂中的分段，称seg_i(tra₁)和seg_i(tra₂)为相似分段，当两个分段之间IP的数量相等；两个分段之间的分段时间的绝对差值小于一个常数，即|(T_i(tra₁)T_i+1(tra₁))-(T_i(tra₂)T_i+1(tra₂))|＜t_p其中(T_i(tra₁)T_i+1(tra₁))为兴趣点列1的分段时间，(T_i(tra₂)T_i+1(tra₂))为兴趣点列2的分段时间，t_p为常数；相似路线，由分段组成，如果有多个连续的相似分段，则为相似路线；假设r_i和r_j是相似路线，则认为两条路线没有区别，即Vdif_vector(r_i(tra₁),r_j(tra₂))＝0，其中r_i(tra₁)为兴趣点列1的路线，r_j(tra₂)为兴趣点列2的路线；下述公式计算轨迹之间的不相似度： dif ( tra 1 , tra 2 ) = Σ i = 1 n p ω i dif vector ( seg i ( tra 1 ) , seg i ( tra 2 ) ) + max { n 1 ex , n 2 ex } ]]> 其中，max{n_1ex,n_2ex}是n_1ex和n_2ex的最大值，n_1ex是tra(1)位于公共点之外的non-COIPs数量，n_2ex是tra(2)位于公共点之外的non-COIPs数量，n_p是用户兴趣点的数量，在tra(1)中有两个位于公共点之外的non-CoIPs，因此n_1ex＝2，tra(2)中位于公共点之外的non-CoIPs的数量为1，n_2ex＝1，因此max{n_1ex,n_2ex}＝2； ω i = ( Len i ( tra 1 ) Len ( tra 1 ) · Len i ( tra 1 ) + Len i ( tra 2 ) Len ( tra 2 ) · Len i ( tra 2 ) ) Len ( tra 1 ) + Len ( tra 2 ) ]]> Len_i(tra₁)表示seg_i(tra₁)的长度，Len(tra₁)是tra₁的长度，Len_i(tra₂)表示seg_i(tra₂)的长度，Len(tra₂)是tra₂的长度，seg_i的距离与长度的含义不同，seg_i(tra₁)的距离是CoIP_i和CoIP_i+1之间的直线距离，而长度是用户从CoIP_i走到CoIP_i+1的路程。