一种基于UG和MATLAB的多自由度注塑机械臂建模方法

本发明公开了一种基于UG和MATLAB的多自由度注塑机械臂建模方法，运用UG的结构表达式驱动和MATLAB的link函数分别建立机械臂的结构模型和D‑H模型，将UG接口的全部操作编译成独立的M函数嵌入到MATLAB/Simulink模块的动态系统仿真模型中进行轨迹曲线的拟合。本发明得到在有限空间约束的条件下轨迹连续，关节平滑，末端运动时间较短，满足实际需求的一条理想轨迹通过协同仿真，以结构动力学和控制系统运动学协同仿真相结合为途径，寻求在有限空间约束下机械臂轨迹优化方法，实现了优化后轨迹关节平滑驱动。

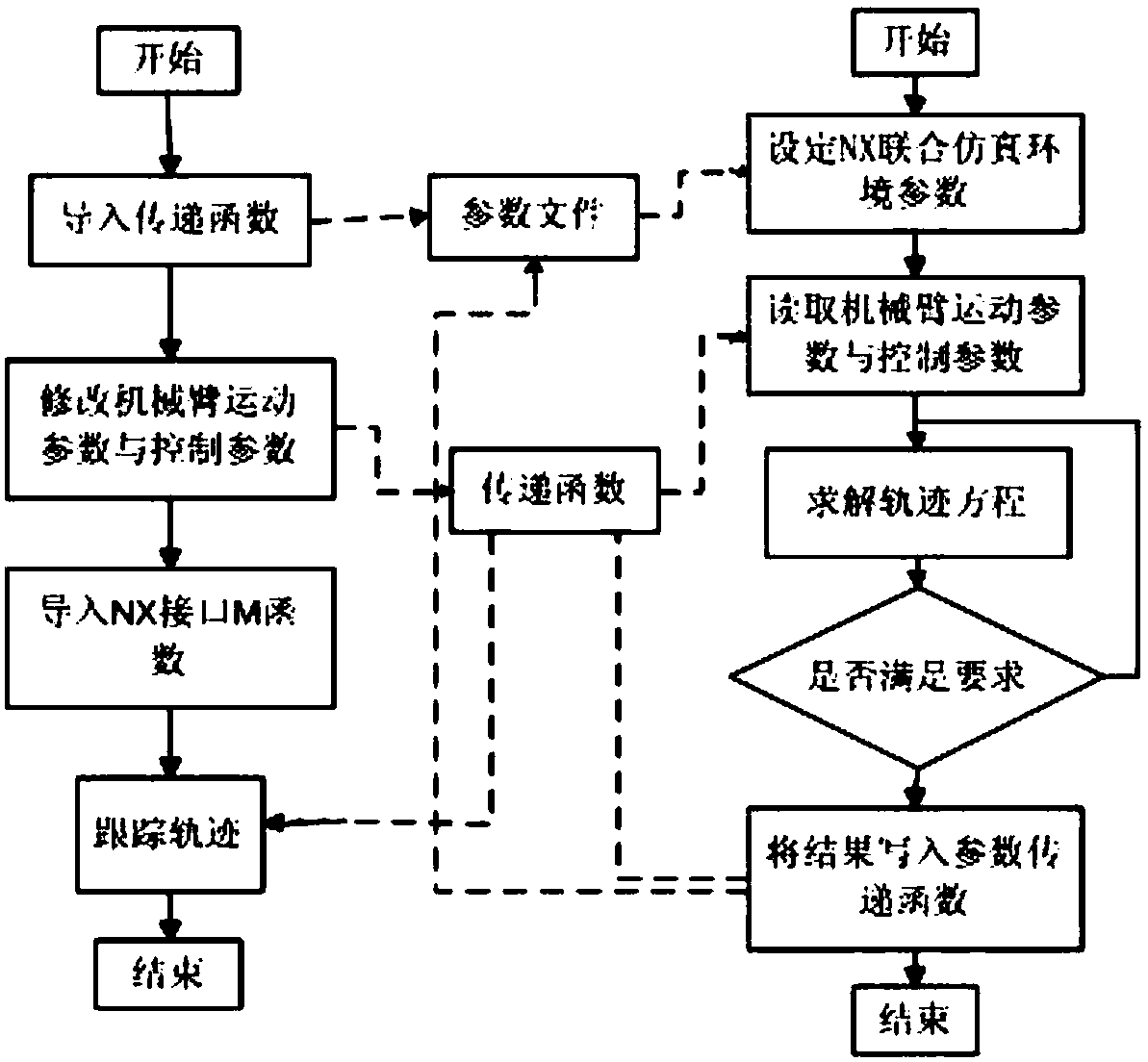
1.一种基于UG和MATLAB的多自由度注塑机械臂建模方法，其特征在于：该方法包括以下步骤：(1)采用UG对多自由度注塑机械臂建立参数化驱动的模型；(2)建立传递函数为M函数，M函数以机械臂的运动参数与控制参数为输入，以机械臂在有限空间的运动轨迹为输出；(3)通过设定GUI参数和修改传递文件，将M函数传递给UG运用MATLAB Robotics Toolboxlink函数建立机械臂运动学模型，并在MATLAB中建立机械臂控制系统运动学方程；(4)在MATLAB中驱动函数得到机械臂各关节位姿，调用drivebot函数可调节控制界面的滑条转动各关节，观察机械臂在空间中运动的轨迹、范围；(5)将UG作为MATLAB/Simulink中的运动分析计算引擎，实时提供机械臂在当前运动参数和控制参数下的运动分析，根据当前运动情况计算下一时刻机械臂的运动参数和控制参数，将MATLAB/Simulink的控制系统模块嵌入到UG中，在每个时间迭代步，计算机械臂的实时运动参数以确定最优轨迹，在协同仿真模式下，NX和MATLAB/Simulink的仿真条件根据当前系统运行条件解算确定。
2.根据权利要求1所述的一种基于UG和MATLAB的多自由度注塑机械臂建模方法，其特征在于：步骤(3)中，在不考虑摩擦力等外界干扰的作用，机械臂的动力学方程为：$D\left(q\right)\stackrel{\·\·}{q}+C(q,\stackrel{\·}{q})\stackrel{\·}{q}+G\left(q\right)=\mathrm{\τ}---\left(8\right)$式中：D(q)—n×n阶对称正定的惯量矩阵；—n×n阶离心力和哥氏力项；G(q)—重力项。基于M函数的Simulink控制器与机械臂的仿真模型函数关系式为：$\mathrm{\τ}=f_0({\stackrel{\·\·}{q}}_d,{\stackrel{\·}{q}}_d,q_d,q,\stackrel{\·}{q})---\left(9\right)$$\stackrel{\·\·}{q}=f_1(q,\stackrel{\·}{q},\mathrm{\τ})---\left(10\right)$式中：τ—控制器输出与受控对象输入的关节驱动力矩/力，q—关节的角速度和角位移；q_d—期望关节轨迹的角加速度，角速度和角位移。$D\left(q\right)=\left[\begin{array}{ccc}{P}_1+P_2+P_3+2P_4\cos q_3& P_2+P_3+P_{4}cos{q}_3& P_3+P_4\cos q_3\\ P_2+P_3+P_{4}cos{q}_3& P_3+P_4\cos q_3& P_4\cos q_3\\ P_3+P_4\cos q_3& P_4\cos q_3& P_3\end{array}\right]$$C(q,\stackrel{\·}{q})=\left[\begin{array}{ccc}-2P_4{\stackrel{\·}{q}}_3\sin q_3& -P_4{\stackrel{\·}{q}}_3\sin q_3& -P_4{\stackrel{\·}{q}}_3\sin q_3\\ P_4{\stackrel{\·}{q}}_2\sin q_3& P_4{\stackrel{\·}{q}}_2\sin q_3& P_4{\stackrel{\·}{q}}_2\sin q_3\\ P_4{\stackrel{\·}{q}}_1\sin q_3& P_4{\stackrel{\·}{q}}_1\sin q_3& 0\end{array}\right]$$G\left(q\right)=\left[\begin{array}{c}{P}_5{\mathrm{gcosq}}_1+P_{6}g\cos (q_1+q_2)+P_{7}g\cos (q_1+q_2+q_3)+P_{8}g\cos \left(q_1\right)\\ P_{6}g\cos (q_1+q_2)+P_{7}g\cos (q_1+q_2+q_3)\\ P_{7}g\cos (q_1+q_2+q_3)\end{array}\right]$P＝[P₁,P₂,P₃,P₄,P₅,P₆,P₇,P₈]为线性后的参数向量式中：P₁＝I₁+m₁r₁²+(m₂+m₃)l₁²；P₂＝I₂+m₂r₂²+m₃(l₁+l₂)²；P₃＝I₃+m₃r₃²；P₄＝m₂r₂l₁+m₃r₃(l₁+l₂)；P₅＝m₁r₁；P₆＝m₂r₂；P₇＝m₃r₃；P₈＝(m₂+m₃)l₁；g—重力加速度。